Introduzione
L’insegnamento della matematica rappresenta una sfida spesso complessa, poiché questa disciplina è spesso percepita come astratta e lontana dalla realtà quotidiana. Tuttavia, grazie all’uso di materiali didattici manipolativi, modelli tridimensionali, strumenti digitali e supporti visivi, è possibile avvicinare gli studenti alla matematica in modo più coinvolgente e comprensibile.
Questi strumenti trasformano concetti apparentemente distanti in esperienze concrete, offrendo un approccio interattivo che può rivoluzionare il modo in cui gli studenti percepiscono e apprendono la matematica.
Attraverso materiali che rendono tangibili nozioni altrimenti astratte, si facilita non solo la comprensione immediata, ma anche l’apprendimento a lungo termine. Questa metodologia promuove inoltre un ambiente educativo inclusivo e adattabile ai diversi stili di apprendimento e alle esigenze specifiche di ciascuno studente.
In questo articolo, esploreremo le varie tattiche per gli studenti della fascia di età 14-18 anni. Scopriremo come integrare questi strumenti nelle classi e approfondiremo l’impatto rivoluzionario di educatori come Emma Castelnuovo, il cui approccio innovativo ha reso la matematica più accessibile.
L’Efficacia di Utilizzare Oggetti Manipolativi Nella Didattica
L’utilizzo di materiali educativi manipolativi nell’insegnamento della matematica è sostenuto da una solida base scientifica, che ne evidenzia i benefici per la comprensione e la memorizzazione dei concetti nel lungo termine. A beneficiarne in particolarmente sono studenti che hanno una predisposizione all’apprendimento tendente al visivo o cinestetico e che dunque faticano con l’astrazione: la manipolazione permette loro di visualizzare e comprendere concetti matematici che altrimenti risulterebbero complessi.
Le teorie cognitive sull’apprendimento suggeriscono che quando gli studenti possono manipolare e sperimentare direttamente con i materiali, la loro comprensione diventa più profonda e duratura. La Teoria del Carico Cognitivo (Sweller, 1988) sottolinea come la mente umana ha dei limiti in termini di attenzione, memoria ed elaborazione. Per tanto, l’apprendimento negli studenti é facilitato quando si riduce il carico cognitivo attraverso strumenti che ne semplificano la comprensione di concetti complessi attraverso tali strumenti.
Secondo Mayer (2001), invece, é il coinvolgimento multisensoriale, come quello offerto dai manipolativi che favorisce la costruzione di connessioni tra rappresentazioni simboliche e concrete. Questo approccio permette agli studenti di “vedere” e “toccare” i concetti astratti, migliorando la comprensione e aiutando a costruire una base più solida per l’apprendimento successivo. Ad esempio, manipolare oggetti fisici come blocchi per rappresentare le frazioni o abachi per esplorare i numeri consente agli studenti di sviluppare una comprensione visiva e pratica dei concetti matematici.
Infine, una meta-analisi condotta da Kul, Çelik e Aksu (2018) ha confermato l’efficacia dei materiali didattici tangibili nell’incrementare i risultati degli studenti in matematica. I ricercatori hanno dimostrato che l’uso di materiali fisici nella didattica non solo migliora la performance, ma riduce anche l’ansia da matematica e la motivazione degli studenti.
Tipologie di Materiali Educativi Fisici e Visivi Nell’Insegnamento.
L’applicazione di materiali educativi fisici può variare in base ai concetti matematici da insegnare e dall’età degli studenti.
Tra i materiali educativi più comuni e utili troviamo i manipolativi concreti, come blocchi, abachi e modelli tridimensionali, che sono particolarmente efficaci per insegnare concetti astratti come frazioni, geometria e algebra di base. E’ stato dimostrato che l’uso regolare di questi strumenti può aumentare la motivazione degli studenti ed il loro l’apprendimento più partecipativo.
Oltre ai manipolativi fisici, esistono strumenti visivi come grafici, diagrammi e modelli geometrici. Questi aiutano gli studenti a visualizzare concetti matematici complessi e a comprendere le relazioni tra diverse quantità o forme geometriche. Sarama e Clements (2009) nella loro ricerca dimostrano l’efficacia di strumenti visivi nel facilitare la comprensione delle relazioni matematiche e concetti più accessibili.
| Tipo di Materiale | Strumenti | Benefici Principali | Esempi |
| Manipolativi Concreti | Blocchi, Lego, Monete, Bicchieri | Comprensione concettuale e visuale delle operazioni e delle relazioni matematiche | Blocchi Lego per rappresentare le frazioni e mostrare la crescita di potenze. |
| Modelli Geometrici | Figure tridimensionali per geometria solida e piana | Facilitano la comprensione di concetti spaziali e delle proprietà geometriche | Sfere, cubi e piramidi per spiegare il volume e la superficie, facendo toccare agli studenti le figure e misurandone i lati. |
| Grafici e Diagrammi | Rappresentazione grafica di funzioni, dati e statistiche | Per la comprensione di relazioni tra variabili e nella risoluzione dei problemi | Creare grafici cartesiani per mostrare l’andamento di funzioni visualizzando la loro inclinazione e curvatura. |
| Strumenti di Misura | Righelli, goniometri, compassi e bilance | Sviluppano competenze pratiche e concrete per applicare la matematica nella vita reale | Misurare oggetti in classe per calcolare il perimetro e l’area, o usare una bilancia per esplorare il concetto di massa e peso. |
| Materiali Visivi | Flashcards, poster, mappe concettuali | Offrono rappresentazioni immediate e semplificate dei concetti matematici e migliorano la memorizzazione | Creare flashcards per memorizzare formule geometriche e concetti chiave come l’area e il volume di forme comuni. |
| Software Interattivi | Programmi e app educative (ad es. GeoGebra) | Incrementano il coinvolgimento e permettono di simulare e visualizzare concetti complessi | Utilizzare GeoGebra per creare rappresentazioni dinamiche di parabole e cerchi, consentendo agli studenti di manipolare i parametri. |
Esempi Pratici: Come Integrare i Materiali Didattici in Classe
Integrare i materiali didattici in modo efficace nelle lezioni di matematica richiede una pianificazione strategica da parte degli insegnanti, che devono considerare i bisogni specifici della classe e gli obiettivi di apprendimento. Quando i materiali sono scelti e utilizzati correttamente, possono aiutare gli studenti a comprendere meglio concetti complessi, promuovere il coinvolgimento e rendere la matematica più accessibile. Vediamo alcune strategie ed esempi pratici su come i materiali manipolativi e visivi possono essere utilizzati per insegnare concetti come frazioni, monomi, insiemistica e potenze.
1. Frazioni
Le frazioni possono essere particolarmente complesse per gli studenti più giovani e non solo, soprattutto perché richiedono la comprensione di parti di un intero. I manipolativi, come i blocchi di un LEGO o i cerchi divisi in parti, permettono agli studenti di visualizzare e manipolare le frazioni. Ad esempio:
Blocchi frazionari: Fai sovrapporre blocchi da 1/4, 1/2, 3/4 per mostrare loro l’evoluzione frazionaria e come formano un intero. Questo li aiuta a comprendere come sommare frazioni con denominatori uguali.
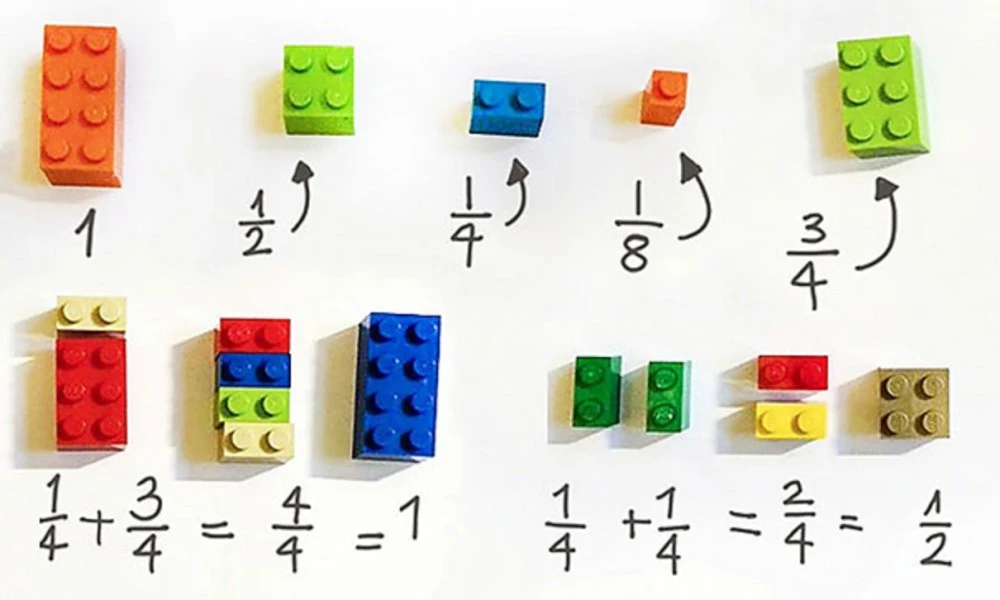
Immagine, Source: https://www.lexilab.it/frazioni-e-simboli-matematici-indesign-essentials/
2. Espressioni Algebrica
I monomi, o espressioni algebriche semplici, sono spesso introdotti al primo anno del biennio della scuola secondaria o terza media. Gli studenti possono trarre beneficio da rappresentazioni visive per migliorare la comprensione. Alcuni esempi includono:
Cos’è una Variabile? Utilizza dei bicchieri per spiegare una variabile. Ogni bicchiere di colore diverso rappresenta una x, y, z. Gli studenti possono riempirli con un liquido o oggetto a loro piacimento e creare una espressione letterale.
Cos’è una Potenza? Successivamente chiedi loro di impilare 3 bicchieri dello stesso colore. Hanno creato una potenza: esempio: x elevato alla terza.
3. Insiemistica
L’insiemistica può essere visualizzata efficacemente utilizzando materiali manipolativi per rappresentare gli insiemi e i loro elementi, rendendo il concetto di insiemi e sottoinsiemi molto più tangibile. Alcuni esempi pratici includono:
Cerchi di cartoncino: come docente o educatore utilizza cerchi di cartoncino colorato per rappresentare insiemi distinti (ad esempio, A e B) ed elementi al loro interno con biglie o bottoni. Spostando questi elementi dentro e fuori i cerchi, gli studenti possono manipolare operazioni come l’unione (A ∪ B) e l’intersezione (A ∩ B).
Diagrammi di Venn: utilizza cerchi di cartoncino o hula hoop o anelli di plastica sovrapposti sul pavimento e poni esempi pratici alla tua classe che coinvolgono i loro interessi. Successivamente chiedi di loro di realizzare un nuovo esempio pratico.
In sintesi, la scelta del tipo di materiale educativo dovrebbe considerare il concetto matematico da insegnare, le caratteristiche dello studente e le risorse disponibili. La miglior strategia? Una combinazione di manipolativi, supporti visivi e strumenti digitali crea un ambiente di apprendimento dinamico e inclusivo, capace di migliorare la comprensione matematica e favorire un apprendimento attivo e duraturo (Carbonneau et al., 2013; Sarama & Clements, 2009). È altrettanto importante che gli insegnanti lascino agli studenti il tempo di riflettere sul compito svolto, consentendo loro di assimilare quanto appreso e di consolidare i concetti in modo profondo. Questo momento di riflessione aiuta a interiorizzare il significato dei materiali utilizzati e a sviluppare una comprensione più solida e consapevole dei contenuti matematici.
Conclusioni
L’utilizzo di risorse didattiche tattili in matematica rappresenta una risorsa preziosa per rendere questa disciplina più accessibile e coinvolgente. L’integrazione di manipolativi, supporti visivi e strumenti digitali facilita la comprensione dei concetti matematici e promuove un ambiente inclusivo, dove ogni studente può avvicinarsi alla matematica in modo concreto e significativo.
La recente letteratura scientifica analizzata evidenzia i molteplici benefici: non solo migliorano i risultati accademici, ma aumentano il coinvolgimento e la fiducia nelle capacità degli studenti, riducendo al contempo l’ansia verso la matematica. Un approccio multisensoriale permette agli studenti di “vedere” e “toccare” la matematica, sviluppando una comprensione più profonda e duratura (Carbonneau et al., 2013; Sarama & Clements, 2009).
È importante, inoltre, che gli insegnanti riservino del tempo alla riflessione post-attività, un momento in cui gli studenti possono consolidare le competenze apprese. Con l’uso mirato di materiali didattici, la matematica può diventare un mondo stimolante da esplorare, comprendere e apprezzare, come dimostrato dal percorso tracciato da educatori come Emma Castelnuovo.
Bibliografia
Carbonneau, K. J., Marley, S. C., & Selig, J. P. (2013). A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. Journal of Educational Psychology, 105(2), 380–400. https://doi.org/10.1037/a0031084
Clements, D. H., & Sarama, J. (2011). Early childhood mathematics education research: Learning trajectories for young children. Routledge.
Furinghetti, F., & Menghini, M. (2014). The role of concrete materials in Emma Castelnuovo’s view of mathematics teaching. Educational Studies in Mathematics, 87, 1–6. https://doi.org/10.1007/s10649-014-9569-8
Kul, Ü., Çelik, S., & Aksu, Z. (2018). The impact of educational material use on mathematics achievement: A meta-analysis study. Educational Research Review, 24, 17–24. https://doi.org/10.1016/j.edurev.2018.03.004
Lorenzoni, F. (2014). Interweaving mathematics with reality and beauty: The valuable legacy of Emma Castelnuovo. Lettera Matematica, 2, 99–102.
Mayer, R. E. (2001). Multimedia learning. Cambridge University Press.
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257–285.
Lascia una risposta