Introduction
Teaching mathematics is often a complex challenge, as this subject is frequently perceived as abstract and disconnected from everyday life. However, with the use of manipulative teaching materials, 3D models, digital tools, and visual aids, it becomes possible to engage students with math in a more interactive and comprehensible way.
These tools transform seemingly distant concepts into concrete experiences, offering an interactive approach that can revolutionize the way students perceive and learn mathematics.
Through materials that make otherwise abstract notions tangible, it facilitates not only immediate understanding but also long-term learning. This methodology also promotes an inclusive educational environment that is adaptable to the different learning styles and specific needs of each student.
In this article, we will explore various tactics for students in the 14-18 age group. We will discover how to integrate these tools into classrooms and delve into the revolutionary impact of educators like Emma Castelnuovo, whose innovative approach has made math more accessible.
The Effectiveness of Using Manipulative Objects in Teaching.
The use of manipulative educational materials in the teaching of mathematics is supported by a solid scientific basis, which highlights their benefits for understanding and memorizing concepts in the long term. Benefiting particularly are students who have a predisposition to learning that tends toward the visual or kinaesthetic and who therefore struggle with abstraction: manipulatives enable them to visualize and understand mathematical concepts that would otherwise be complex.
Cognitive theories of learning suggest that when students can directly manipulate and experiment with materials, their understanding becomes deeper and more enduring. Cognitive Load Theory (Sweller, 1988) emphasizes how the human mind has limitations in terms of attention, memory and processing. Therefore, learning in students is facilitated when cognitive load is reduced through tools that simplify their understanding of complex concepts through such tools.
According to Mayer (2001), however, it is multisensory engagement, such as that offered by manipulatives that fosters the building of connections between symbolic and concrete representations. This approach allows students to “see” and “touch” abstract concepts, enhancing understanding and helping to build a stronger foundation for later learning. For example, manipulating physical objects such as blocks to represent fractions or abacuses to explore numbers allows students to develop a visual and hands-on understanding of mathematical concepts.
Finally, a meta-analysis conducted by Kul, Çelik and Aksu (2018) confirmed the effectiveness of tangible teaching materials in increasing student achievement in mathematics. The researchers showed that the use of physical materials in teaching not only improves performance, but also reduces students’ math anxiety and motivation.
Types of Physical and Visual Educational Materials In Teaching.
The application of physical educational materials may vary depending on the mathematical concepts to be taught and the age of the students.
Among the most common and useful educational materials are concrete manipulatives, such as blocks, abacuses and three-dimensional models, which are particularly effective for teaching abstract concepts such as fractions, geometry and basic algebra. It has been shown that regular use of these tools can increase students’ motivation and their more participatory learning.
In addition to physical manipulatives, there are visual tools such as graphs, diagrams and geometric models. These help students visualize complex mathematical concepts and understand relationships between different quantities or geometric shapes. Sarama and Clements (2009) in their research demonstrate the effectiveness of visual tools in facilitating understanding of mathematical relationships and more accessible concepts.
| Type of Material | Tools | Main Benefits | Examples |
| Concrete Manipulatives | Blocks, LEGO, Coins, Tumblers | Conceptual and visual understanding of mathematical operations and relationships | LEGO blocks to represent fractions and show growth of powers. |
| Geometric Models | Three-dimensional figures for solid and plane geometry | Facilitate understanding of spatial concepts and geometric properties | Spheres, cubes and pyramids to explain volume and surface area by having students touch the figures and measure their sides. |
| Graphs and Diagrams | Graphical representation of functions, data and statistics | For understanding relationships between variables and in problem solving | Create Cartesian graphs to show the progress of functions by visualizing their slope and curvature. |
| Measuring Instruments | Rulers, protractors, compasses and scales | They develop practical, concrete skills for applying mathematics in real life | Measure objects in class to calculate perimeter and area, or use a scale to explore the concept of mass and weight. |
| Visual Materials | Flashcards, posters, concept maps | Offer immediate and simplified representations of mathematical concepts and improve memorization | Create flashcards to memorize geometric formulas and key concepts such as area and volume of common shapes. |
| Interactive Software | Educational programs and apps (e.g., GeoGebra) | They increase engagement and allow simulation and visualization of complex concepts | Use GeoGebra to create dynamic representations of parabolas and circles, allowing students to manipulate parameters. |
Practical Examples: How to Integrate Instructional Materials in the Classroom.
Integrating instructional materials effectively into mathematics lessons requires strategic planning by teachers, who must consider specific classroom needs and learning objectives. When materials are chosen and used correctly, they can help students better understand complex concepts, promote engagement, and make mathematics more accessible. Let’s take a look at some strategies and practical examples of how manipulative and visual materials can be used to teach concepts such as fractions, monomials, set theory, and powers.
1. Fractions
Fractions can be particularly complex for younger students and beyond, especially since they require understanding parts of a whole. Manipulatives, such as blocks in a LEGO or circles divided into parts, allow students to visualize and manipulate fractions. For example:
Fractional Blocks: Have them overlap 1/4, 1/2, 3/4 blocks to show them fractional evolution and how they form a whole. This helps them understand how to add fractions with equal denominators.
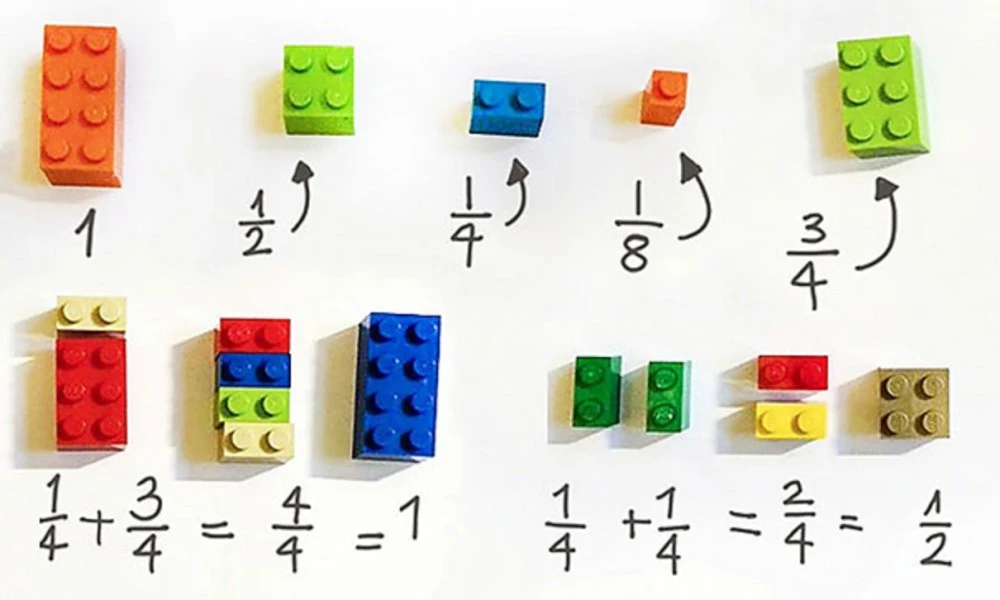
Source: https://www.lexilab.it/frazioni-e-simboli-matematici-indesign-essentials/
2. Algebraic Expressions
Monomials, or simple algebraic expressions, are often introduced in the first year of the two-year secondary school or eighth grade. Students can benefit from visual representations to enhance understanding. Some examples include:
What is a Variable? Use glasses to explain a variable. Each different colored glass represents an x, y, z. Students can fill them with any liquid or object they like and create a literal expression.

What is a Power? Next ask them to stack 3 glasses of the same color. They created a power: example: x raised to the third.

3. Insiemistics
Set theory can be visualized effectively by using manipulative materials to represent sets and their elements, making the concept of sets and subsets much more tangible. Some practical examples include:
Cardboard circles: as a teacher or educator uses colored cardboard circles to represent distinct sets (e.g., A and B) and elements within them with marbles or buttons. By moving these elements in and out of the circles, students can manipulate operations such as union (A ∪ B) and intersection (A ∩ B).
Venn Diagrams: use cardboard circles or hula hoops or plastic rings stacked on the floor and pose practical examples to your class that involve their interests. Next ask them to make a new practical example.
In summary, the choice of the type of educational material should consider the mathematical concept to be taught, the characteristics of the student, and the resources available. The best strategy? A combination of manipulatives, visual aids, and digital tools creates a dynamic and inclusive learning environment that can enhance mathematical understanding and foster active and sustained learning (Carbonneau et al., 2013; Sarama & Clements, 2009). It is equally important for teachers to allow students time to reflect on the task at hand, allowing them to assimilate what they have learned and consolidate concepts in a deep way. This time for reflection helps internalize the meaning of the materials used and develop a more solid and informed understanding of mathematical content.
Conclusions
The use of tactile teaching resources in mathematics is a valuable resource for making this discipline more accessible and engaging. The integration of manipulatives, visual aids, and digital tools facilitates understanding of mathematical concepts and promotes an inclusive environment where every student can approach mathematics in a concrete and meaningful way.
Recent scientific literature reviewed highlights the multiple benefits: not only do they improve academic achievement, but they increase students’ engagement and confidence in their abilities, while reducing anxiety toward mathematics. A multisensory approach allows students to “see” and “touch” mathematics, developing a deeper and more lasting understanding (Carbonneau et al., 2013; Sarama & Clements, 2009).
It is also important for teachers to set aside time for post-activity reflection, a time when students can consolidate the skills they have learned. With the purposeful use of instructional materials, mathematics can become a stimulating world to explore, understand and appreciate, as demonstrated by the path charted by educators such as Emma Castelnuovo.
Bibliography
Carbonneau, K. J., Marley, S. C., & Selig, J. P. (2013). A meta-analysis of the effectiveness of teaching mathematics with concrete manipulatives. Journal of Educational Psychology, 105(2), 380-400. https://doi.org/10.1037/a0031084
Clements, D. H., & Sarama, J. (2011). Early childhood mathematics education research: Learning trajectories for young children. Routledge.
Furinghetti, F., & Menghini, M. (2014). The role of concrete materials in Emma Castelnuovo’s view of mathematics teaching. Educational Studies in Mathematics, 87, 1–6. https://doi.org/10.1007/s10649-014-9569-8
Kul, Ü., Çelik, S., & Aksu, Z. (2018). The impact of educational material use on mathematics achievement: A meta-analysis study. Educational Research Review, 24, 17–24. https://doi.org/10.1016/j.edurev.2018.03.004
Lorenzoni, F. (2014). Interweaving mathematics with reality and beauty: The valuable legacy of Emma Castelnuovo. Lettera Matematica, 2, 99–102.
Mayer, R. E. (2001). Multimedia learning. Cambridge University Press.
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257–285.


Leave a Reply